O princípio de medição considera uma tubulação com comprimento L, diâmetro interno D e área transversal da parede A, com uma extremidade engastada na parede. No interior do tubo escoa um fluido com vazão Q. Através de uma curva colocada na outra extremidade da tubulação, a direção do
escoamento de fluido é desviada, conforme mostra a Fig. 20. Pelo teorema do momentum, uma força F é exercida sobre a tubulação, dando origem a uma tração que tende a aumentar seu comprimento de um valor ΔL. Estas variáveis podem ser relacionadas pela Eq. (10)
onde E é o módulo de elasticidade do material da tubulação.
Desprezando-se a perda de carga no escoamento do fluido pela tubulação e, aplicando-se o teorema do momentum, a seguinte expressão pode ser escrita:
onde ρ é a massa específica do fluido e V é a velocidade média na seção.
Por outro lado, a relação básica do extensômetro resistivo pode ser expressa
como:
onde,
C é a constante do extensômetro (em torno de 2) Δ r é a variação da resistência do extensômetro
r é a resistência do extensômetro não deformado (usualmente 120 Ω)
Relacionando-se as Eq. (10), (11) e (12) pode-se obter uma relação entre a variação da resistência como função da vazão.
Um raciocínio semelhante pode ser utilizado para a deformação da curva do medidor.
Variação da resistência do extensômetro
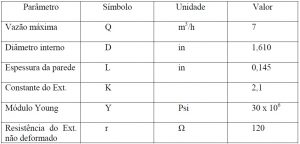
Tabela 1: Valores dos parâmetros para projeto
Para o projeto do sistema de medição, os valores da tabela 1 foram utilizados, correspondentes à máxima vazão encontrada em campo, nos sistemas de refrigeração da Usina, para uma tubulação de 1,5 in (3,81mm) nominal.
Usando as Eq. (10), (11) e (12), juntamente com os dados da Tabela 1, os seguintes parâmetros podem ser calculados.
Tabela 2: Parâmetros Calculados
 Uma amplificação do sinal resultante foi conseguida através do uso de dois tipos básicos de circuitos :
Uma amplificação do sinal resultante foi conseguida através do uso de dois tipos básicos de circuitos :
• Divisor de tensão.
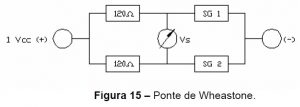
• Ponte de Wheatstone.
Um equipamento que foi desenvolvido para viabilizar estas medições consta de uma ponte de Wheatstone, conforme ilustrado na Fig. 15, com duas resistências fixas no valor de 120 Ω cada, um extensômetro não deformado com resistência de 120 Ω e, um outro, com igual resistência para medir a deformação.
A ponte foi alimentada por uma corrente constante I. A diferença de tensão (ΔV) entre dois vértices da ponte é proporcional à diferença de resistência dos extensômetros (Δr) e à corrente, conforme a expressão:
Usando-se a variação de resistência calculada para a Tabela 2, a tensão pôde ser determinada pela Eq. (13) e amplificada, para que pudesse ser lida por um microvoltímetro.
Referências Técnicas
Parte deste texto se baseia na seguinte referência, onde informações adicionais podem ser obtidas:
PUC-Rio – Certificação Digital Nº 0513367/CA